Rational Numbers are Countable

We can prove this easily if we note that \(\mathbb{N} \times \mathbb{N}\) is countable, and \(\mathbb{Z}\) is countable, by then just composing injections \(\mathbb{Q} \hookrightarrow \mathbb{Z} \times \mathbb{Z} \hookrightarrow \mathbb{N} \times \mathbb{N}\). Here we present a more elementary proof though.

Proof

Consider presenting all of the positive rational numbers in a rectangular array by increasing the numerator to the left and the denominator going downwards.

Listing these horizontally does not work, since if we choose a number in the second row for example, because the first row is infinite, that selected element will never be reached. As such, we must list diagonally as follows:

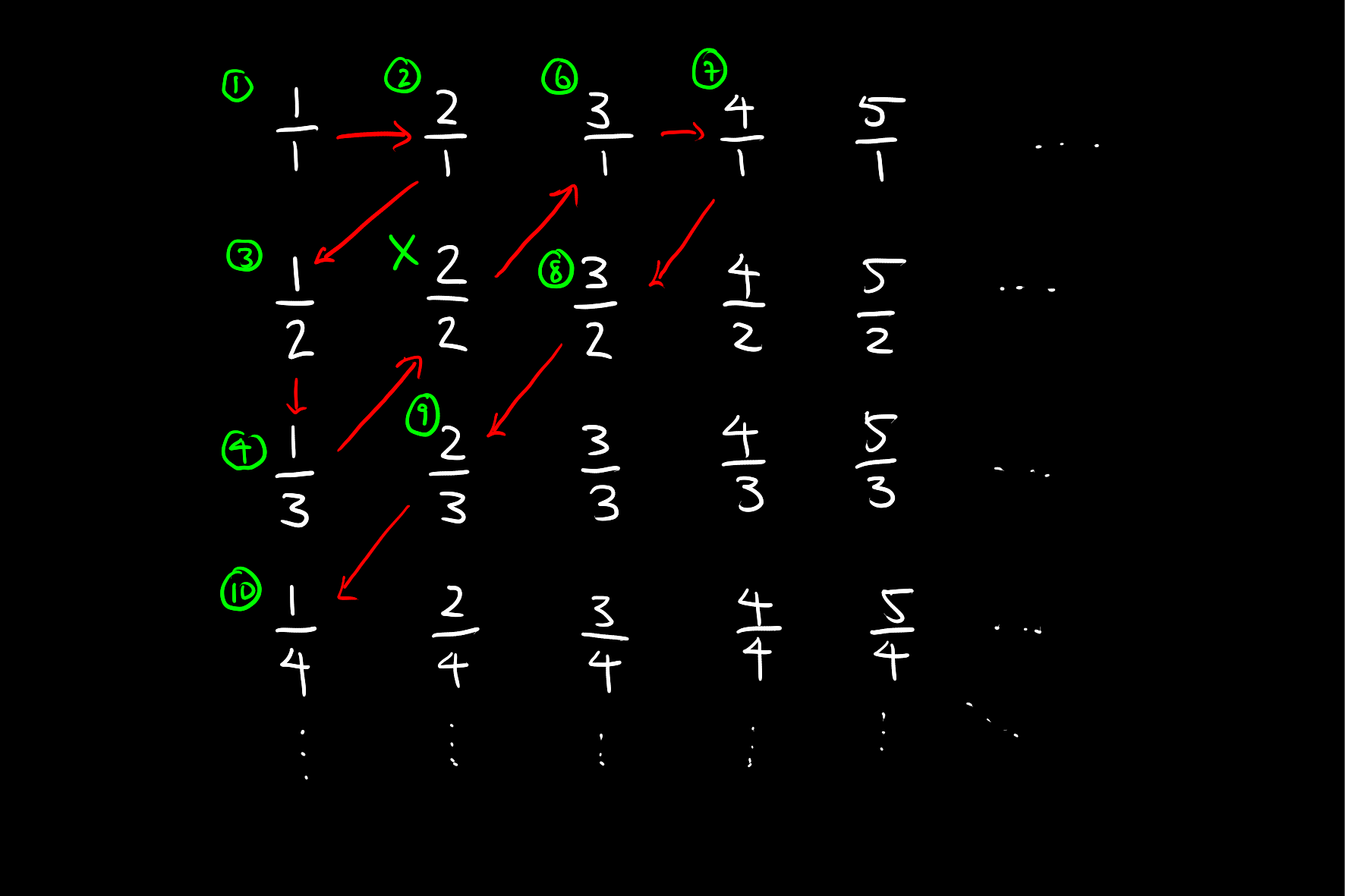
We can then proceed diagonally as above, skipping any rational number which has already been covered. By assigning an index to each element in the index starting at \(0\), we have constructed a bijection between \(\mathbb{Q}^{+}\) and \(\mathbb{N}\), thus proving that \(\mathbb{Q}^{+}\) is countable.

Then, the function \(x \mapsto -x\) gives a bijection from \(\mathbb{Q}^{+}\) to \(\mathbb{Q}^{-}\), thus proving that \(\mathbb{Q}^{-}\) is countable.

Finally, expressing the rational numbers as:

and noting that the countable union of countable sets is countable, we have that \(\mathbb{Q}\) is countable.